二次元
二次元の場合には,
\(\Large P_2 (r, t) = \frac{1}{4 \pi D t} e^{- \frac{r^2}{4Dt}} \)
となるのですが,そのまま r=0 to ∞,としても計算結果が1となりません.
それは,一次元の場合には確率密度を積分すればいいのですが,二次元以上となると中心からの距離rによって占有するエリア(面積,体積)が変わってくるからです.

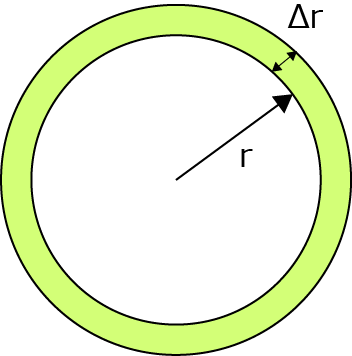
この緑色の面積がrによってどう変わるかを計算すると,
\(\Large \begin{align*} S (r, \Delta r) &= \pi ( r + \Delta r)^2 - \pi r^2 \\
&= \pi \left( r^2+2r \cdot \Delta r + \Delta r^2 - r^2 \right) \\
&=
\pi \left( 2r \cdot \Delta r + \Delta r^2 \right) \\
&\simeq 2 \pi r \cdot \Delta r
\end{align*} \)
となりますので,
粒子数=密度×面積
から,
\(\Large \int_{0}^{\infty} 2 \pi r \frac{1}{4 \pi D t} e^{- \frac{r^2}{4Dt}} dr \)
を計算することになります(積分範囲が0から∞になっていることに注意).
\(\Large \begin{align*} & \int_{0}^{\infty} 2 \pi r \frac{1}{4 \pi D t} e^{- \frac{r^2}{4Dt}} dr \\
&= \frac{1}{2Dt} \int_{0}^{\infty} r e^{- \frac{r^2}{4Dt}} dr \\
\end{align*} \)
ここで,
\(\Large \frac{d}{dr} e^{- \frac{r^2}{4Dt}} = - \frac{2r}{4Dt} e^{- \frac{r^2}{4Dt}} \)
となるので,
\(\Large r e^{- \frac{r^2}{4Dt}} = -2Dt \frac{d}{dr} e^{- \frac{r^2}{4Dt}} \)
となります.従って,
\(\Large \begin{align*} & \frac{1}{2Dt} \int_{0}^{\infty} r e^{- \frac{r^2}{4Dt}} dr \\
&= \frac{1}{2Dt} \int_{0}^{\infty}\left( -2Dt \frac{d}{dr} e^{- \frac{r^2}{4Dt}} \right) dr \\
&= - \left[
e^{- \frac{r^2}{4Dt}} \right]_0^{\infty} \\
&=
- \left[ 0-1 \right]_0^{\infty} \\
&= 1
\end{align*} \)
となり,規格化されていることがわかります.
次ページに三次元の場合を考えていきましょう.